Para aqueles que não sabem o que é um ângulo raso ou de meia-volta, esse artigo pode ser de muita ajuda. Aqui verá o significado, conceito e definição desse termo que é muito usado na geometria e na trigonometria. Também verá qual o seno, cosseno e tangente desse ângulo, segundo a Wikipédia.
Entretanto, para fixar esse conteúdo, será de extrema importância a resolução de exercícios. Pois, somente assim, é possível guardar na sua mente o significado de cada um dos termos usados nessa matéria que é muito complexa e causa muitos problemas a vários estudantes.

O que é um ângulo raso ou de meia-volta?
É aquele que mede, exatamente, 180º.
Ele é chamado, também, de meia volta pois é formado por duas semirretas com direções opostas que possuem a mesma origem. Apresentando o dobro de graus que um ângulo reto.
Mais abaixo poderá ver o passo a passo para fazer o desenho do mesmo no seu trabalho escolar ou na sua atividade. Pois, assim, terá mais facilidade de entender o funcionamento do ângulo raso ou de meia-volta.
Seno de 180º
O seno é 0.
Cosseno 180º
O cosseno é -1.
Tangente 180º
A tangente é 0. Isso porquê a tangente é igual ao seno dividido pelo cosseno.
Como desenhar um Ângulo Raso ou de Meia-Volta?
Para desenhar um ângulo raso ou de meia-volta deve-se fazer o seguinte:
- desenhe um ponto de referência;
- desenhe uma reta para um dos lados;
- desenhe outra reta para o lado oposto, sendo que essa reta deve parecer complementar à primeira;
- faça um semicírculo de 180º ao redor do ponto, de maneira com que comece em uma das semirretas e termine na outra ;
- indique o número do ângulo que está desenhando(180º).
O resultado que produzirá será semelhante à imagem abaixo:
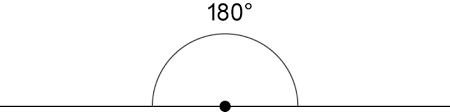
Deu para você entender qual a definição de ângulo raso ou de meia-volta? Deixe-nos um comentário com dúvidas, sugestões ou possíveis erros para que possamos ajudar um maior número de pessoas com esse artigo.