Existem várias áreas na matemática, dentre elas podemos destacar a trigonometria e a geometria. Essas são as áreas responsáveis pelos estudos de figuras geométricas e seus ângulos. E é através delas que podemos saber o conceito sobre o que é ângulo reto. Sendo esse tema um dos principais estudos dessas duas áreas importantíssimas para pessoas de exatas como engenheiros e matemáticos.
Também é preciso saber, além desse significado, o seno, o cosseno e a tangente do ângulo reto. Aqui verá um pouco sobre esse tema de maneira simples e poderá tirar uma melhor nota nas suas disciplinas de exatas.
O que é Ângulo Reto?
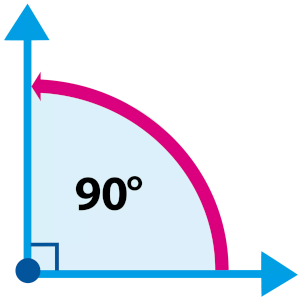É um ângulo de 90º que consiste em um quarto de volta ao redor de um ponto. Uma volta completa ao redor de um ponto possui 360º.
Também pode ser identificado como sendo o menor ângulo entre duas retas perpendiculares. Isso porque é um termo derivado do latim “angulus rectus”, onde reto significa uma reta vertical sobre outra horizontal.
Conceitos importantes e intimamente relacionados com esse termo são a perpendicularidade(que possui relação com o estudo da intersecção entre duas retas) e a ortogonalidade(que possui relação com o estudo de vetores).
Além disso, é considerado um dos ângulos notáveis da trigonometria, visto que possui valores de seno, cosseno e tangente bem definidos como pode ver mais abaixo.
Mas esses são assuntos para outro artigo, não é mesmo?!
Valor do Seno de 90º
O valor do seno de 90º é 1.
Valor do Cosseno de 90º
O valor do cosseno de 90º é 0.
Valor do Tangente de 90º
A tangente de 90º não existe pois a mesma é o resultado da divisão do seno pelo cosseno.
Representação do Ângulo Reto em desenhos
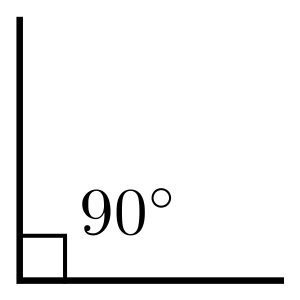
Sempre que houver um ângulo reto, ou seja, o encontro de duas linhas perpendiculares uma a outra em um mesmo ponto, deve-se representar o mesmo com um quadrado, diferentemente da forma como se representa os outros ângulos com um semicírculo. Isso foi convencionado e é uma forma inteligente de diferenciá-lo dos demais em seus desenhos.
Veja abaixo como fazer essa representação no desenho geométrico:
Então, agora que já sabe bastante sobre o tema, faça exercícios e, depois que estiverem resolvidos, volte aqui para comentar sobre o que achou desse artigo sobre o ângulo reto. Bons estudos!