Uma equação do segundo grau é aquela do tipo ax²+bx+c=0, onde a, b e c são constantes reais e a≠0. Mas, não basta saber o que é, é preciso saber como resolver uma equação do 2º grau completa e incompleta.
Para fazer essa resolução existem várias metodologias. A mais ensinada é a fórmula de Bhaskara, que permite encontrar as raízes ou soluções de qualquer equação do tipo, seja ela completa ou incompleta. Porém, para as incompletas, existem metodologias mais simplificadas como as que verá nesse artigo.

Como resolver uma equação do 2º grau completa passo a passo
Esse tipo de equação apresenta a, b, e c diferentes de zero. Por isso é chamada de completa.
Como já dito na introdução, existem várias metodologias para tal. Porém a que as pessoas mais utilizam é a fórmula de Bhaskara. Aqui poderá seguir o passo a passo para resolver esse tipo de questão:
1 – Encontre as incógnitas
O primeiro passo na resolução é encontrar os valores de a, b e c. Pode ser que seja preciso fazer algumas manipulações para que se chegue ao formato ax²+bx+c=0 e possa identificar todos os coeficientes.
Por exemplo:
2x² – 3x + 5 = 1= x² + 2x -1 ⇨ 2x² – x² – 3x – 2x + 5 + 1 ⇨ x² – 5x + 6 = 0
Com essa manipulação, podemos verificar o valor dos coeficientes:
- a = 1
- b = – 5
- c = 6
Com os coeficientes em mãos, já podemos proceder para o próximo item.
2 – Ache o valor do discriminante na fórmula de Delta
![]()
Sabemos que a fórmula de delta é: Δ = b² – 4ac. Então basta substituir os valores na equação para encontrar o valor do discriminante.
Segundo o exemplo do item 1:
Δ = b² – 4ac ⇨ Δ = (-5)² – 4 x 1 x 6 = 25 – 24 = 1
Então temos que Δ = 1 para o exemplo que estamos resolvendo.
Obs.: Aqui devemos fazer um estudo para o valor encontrado em Δ. Se ele for menor que zero não temos raízes reais, se ele for igual a zero temos duas raízes reais e iguais e se ele for maior que zero teremos duas raízes reais e diferentes. Como Δ = 1 no exemplo, então, teremos duas raízes reais e diferentes entre si.
3 – Substitua os valores na fórmula de Bhaskara para obter os resultados
O discriminante é integrante da fórmula de Bhaskara, porém e ele é calculado separadamente para que se possa fazer uma análise das raízes e, também, para que não tenha-se que ficar repetindo toda a fórmula de maneira necessária. Com o valor de Δ em mãos, podemos achar as raízes segundo a fórmula abaixo:
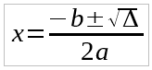
Então a equação ficará assim, substituindo os valores:
x = [ – ( -5 ) ± √1 ] / (2 x 1) ⇨ x = ( 5 ± 1) / 2. Observe que ± não representa uma operação matemática válida, apenas indica que existem as duas opções que, nesse caso, gerará duas soluções reais e diferentes:
x’ = ( 5 + 1) / 2 ⇨ x’ = 6 / 2 ⇨ x’ = 3
x” = ( 5 – 1) / 2 ⇨ x” = 4 / 2 ⇨ x” = 2
Logo as soluções para a equação do 2º grau x² – 5x + 6 = 0 é: x’ = 3 e x” = 2. Para verificar se essas são realmente as soluções, basta substituir os valores encontrados no lugar da variável x na equação dada.
Como resolver uma equação do 2º grau incompleta passo a passo
Existem três tipos de equação do segundo grau incompletas. Todas elas podem ser resolvidas utilizando a fórmula de Bhaskara, usando as técnicas mais acima. Porém não é a forma mais rápida de se fazer isso.
Visando esse tema, poderá ver abaixo a forma mais fácil de resolver cada uma delas sem utilizar-se da fórmula de Bhaskara:
Caso 1: b = 0
Nesse caso a resolução dse dá de maneira simples, basta saber extrair a raiz quadrada de maneira correta.
Veja o seguinte exemplo:
x² – 4 = 0 ⇨ x² = 4 ⇨ √x² = √4 ⇨ | x | = 2 ⇨ x = ± 2.
Então, para esse exemplo, temos como raízes: x’ = – 2 e x” = 2.
Caso 2: c = 0
Nesse caso devemos usar uma manipulação que vem das propriedades da multiplicação que é a fatoração. Mas é bem simples de se fazer isso.
Veja o seguinte exemplo:
x² – 4x = 0 ⇨ x(x – 4) = 0 ⇨ x = 0 ou x – 4 = 0 ⇨ x = 0 ou x = 4.
Então, para esse exemplo, temos como raízes: x’ = 0 e x” = 4.
Caso 3: b = 0 e c = 0
Esse caso é o mais simples de todo pois sempre terá como solução duas raízes reais e iguais a 0.
Veja abaixo um exemplo:
25x² = 0 ⇨ x² = 0/25 ⇨ x² = 0 ⇨ √x² = √0 ⇨ | x | = 0 ⇨ x = ± 0
Então, para esse exemplo, temos como raízes: x’ = 0 e x” = 0.
Teste sempre as respostas nos exercícios
Não basta saber como resolver uma equação do 2º grau, é preciso ter em mente que é preciso testar as respostas sempre que fizer exercícios para averiguar se as respostas encontradas são realmente soluções.
Para isso basta substituir os resultados encontrados pelo valor de x e ver se chegará a uma igualdade válida. Podemos ver isso no primeiro exemplo aqui dado:
x² – 5x + 6 = 0 com raízes x’ = 3 e x” = 2
Testando para x’ = 3
x² – 5x + 6 = 0 ⇨ 3² – (5 x 3) + 6 = 0 ⇨ 9 – 15 + 6 = 0 ⇨ 0 = 0 ✔️
Testando para x” = 2
x² – 5x + 6 = 0 ⇨ 2² – (5 x 2) + 6 = 0 ⇨ 4 – 10 + 6 = 0 ⇨ 0 = 0 ✔️
Como as soluções fazem sentido, logo, de fato, elas são raízes da equação do segundo grau dada.