A Fórmula de Bhaskara e Delta é uma das mais faladas na matemática, inclusive gerando vários memes sobre o tema. Através dela é possível encontrar a solução de equações do segundo grau(também chamadas de equações quadráticas). Por isso ela é uma fórmula muito importante em todo o mundo e auxilia muitos estudantes a encontrarem a solução de uma equação de grau 2.
Embora isso seja verdade, muitas pessoas possuem dificuldades de saber como deduzir a fórmula ou, mesmo, de resolver equações com esse método que é bem simples quando comparado a outros. Então você deve aprender a utilizar a Fórmula de Bhaskara e Delta para conseguir resolver problemas matemáticos.

Fórmula de Bhaskara e Delta
Dada uma equação do 2º grau sendo ax² + bx + c = 0, com a≠0. Podemos usar a seguinte equação para a sua resolução:
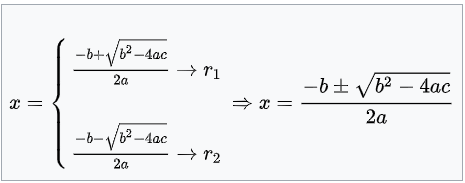
Fórmula de Delta ou Discriminante
Acima temos a fórmula do Bhaskara completa, porém costuma-se calcular delta separado para, posteriormente, colocar na fórmula geral. Delta possui a seguinte fórmula:
![]()
Dessa forma poderá fazer o estudo do sinal e já saber qual o número de raízes reais que a equação possuirá. O estudo do sinal será o seguinte:
- Δ < 0 ⇨ possui apenas raízes imaginárias, sendo assim, não possui raízes reais
- Δ = 0 ⇨ possui duas raízes reais e iguais entre si
- Δ > 0 ⇨ possui duas raízes reais e diferentes entre si
Com esse estudo você já conseguirá saber de antemão o que esperar das soluções da equação do segundo grau dada.
Dedução da Fórmula de Bhaskara
A dedução matemática da mesma pode se dar através do método abaixo:

O que fazer para lembrar-se sempre?
Na hora de resolver uma equação do segundo grau siga o passo a passo abaixo:
- copie a fórmula de Bhaskara em cada exercício;
- encontre o valor do discriminante ou delta e estude as raízes que podem ser obtidas;
- substitua a fórmula no resto da equação e encontre as soluções;
- substitua as soluções na equação original e veja se faz sentido para poder, assim, confirmar que está certo.
Fazendo vários exercícios e seguindo esse passo a passo será mais fácil de se lembrar e poderá tirar uma nota melhor na prova que você for fazer.